Old Ruby vs New Clojure

read

Some years ago I made a program to solve the following problem:

Given the letters in this box, make as many words as possible where the center letters has to be included.

Game Box

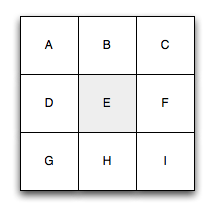
At the time I was coding Ruby but I had done mostly rails development and hadn't really gotten into thinking that much recursively yet. In an afternoon I came up with this code:

def init_wordlist()
  @wordlist = {}
  
  file = File.new("sv_SE.dic", "r")
  while content = file.gets
    @wordlist[content.split("/")[0]] = 1
  end
  file.close
end

def get_permutations(letters)
  permutations = []
  if letters.size == 1
    permutations << letters.first
  else
    letters.each_with_index do |letter, i|
      surrounding_letters = letters.dup; surrounding_letters.delete_at(i)
      permutations += get_permutations(surrounding_letters).map { |permutation| letter + permutation }
    end
  end
  return permutations
end

def generate_combinations(arr)
  combinationshash = {}
  for i in (4..9)
    combinationshash[i] = []
  end
  for i in (0..arr.size-8)
    for j in (i+1..arr.size-7)
      for k in (j+1..arr.size-6)
        for l in (k+1..arr.size-5)
          for m in (l+1..arr.size-4)
            for n in (m+1..arr.size-3)
              for o in (n+1..arr.size-2)
                for p in (o+1..arr.size-1)
                  combinationshash[8] << get_permutations([arr[i], arr[j], arr[k], arr[l], arr[m], arr[n], arr[o], arr[p]])
                end
              end
            end
          end
        end
      end
    end
  end
  
  for j in (0..arr.size-7)
    for k in (j+1..arr.size-6)
      for l in (k+1..arr.size-5)
        for m in (l+1..arr.size-4)
          for n in (m+1..arr.size-3)
            for o in (n+1..arr.size-2)
              for p in (o+1..arr.size-1)
                combinationshash[7] << get_permutations([arr[j], arr[k], arr[l], arr[m], arr[n], arr[o], arr[p]])
              end
            end
          end
        end
      end
    end
  end



  for k in (0..arr.size-6)
    for l in (k+1..arr.size-5)
      for m in (l+1..arr.size-4)
        for n in (m+1..arr.size-3)
          for o in (n+1..arr.size-2)
            for p in (o+1..arr.size-1)
              combinationshash[6] << get_permutations([arr[k], arr[l], arr[m], arr[n], arr[o], arr[p]])
            end
          end
        end
      end
    end
  end


  for l in (0..arr.size-5)
    for m in (l+1..arr.size-4)
      for n in (m+1..arr.size-3)
        for o in (n+1..arr.size-2)
          for p in (o+1..arr.size-1)
            combinationshash[5] << get_permutations([arr[l], arr[m], arr[n], arr[o], arr[p]])
          end
        end
      end
    end
  end

  for m in (0..arr.size-4)
    for n in (m+1..arr.size-3)
      for o in (n+1..arr.size-2)
        for p in (o+1..arr.size-1)
          combinationshash[4] << get_permutations([arr[m], arr[n], arr[o], arr[p]])
        end
      end
    end
  end
  
  combinationshash[9] = get_permutations(arr)
  @nmbr_of_words = 0
  for i in (4..9)
    combinationshash[i].flatten!
    @nmbr_of_words += combinationshash[i].size
  end
  return combinationshash
end


def get_all_words(letters, required)
  lookups = 0
  puts "Beräknar permutationer"
  permutationhash = generate_combinations(letters)
  puts @nmbr_of_words.to_s + " permutationer fanns"
  puts "Slår upp ord"
  words = []
  
  for i in (4..9)
    puts "Ord med " + i.to_s + " bokstäver"
    permutationhash[i].each do |permutation|
      unless (words.include?(permutation))
        lookups += 1 if permutation.include?(required)
        if(permutation.include?(required) && @wordlist[permutation] != nil)
          words << permutation
        end
      end
    end
  end
  puts "Gjorde " + lookups.to_s + " uppslag i ordlistan\n\n"
  return words
end

init_wordlist()
puts "Bokstäver:"
letters = gets
puts "Obligatorisk:"
required = gets
puts "\n"

all_words = get_all_words(letters.split(//)[0..-2], required[0..-2])
puts "Ord som kunde skapas:"
all_words.each_with_index do |word, i| 
  puts "" + (i+1).to_s + ": " + word
end

I have just started playing around with Clojure so I wanted to see if I could make an elegant solution in Clojure and I think I got pretty close.

(ns svd.core
  (:use 
    clojure.contrib.combinatorics)
  (:require
   [clojure.contrib.duck-streams :as ds]
   [clojure.contrib.str-utils :as str]))

(defn wordlist []
  (set (map #(re-find #"[^/]*" %) (ds/read-lines "sv_se.dic"))))

(defn get-all-words [letters required]
  (let [perms (map #(apply str %)
           (filter #(contains? (into #{} %) required)
              (mapcat permutations 
                  (mapcat #(combinations letters %) 
                      '(4 5 6 7 8 9)))))
    words (wordlist)]
    (filter #(contains? words %) perms)))

(defn main [letters required]
  (let [words (get-all-words 
           (into #{} letters)
           (. required charAt 0))]
    (println (str "Hittade " (count words) " ord."))
    (loop [n 1]
      (if (not (> n (count words)))
    (do
      (println (str n ". " (nth (sort-by #(count %) words) (- n 1))))
      (recur (+ n 1)))))))

I really think I've developed a bit as a programmer since then.

Old Ruby vs New Clojure

Written by

Fredrik Olsen

Supported by